- Variable aleatoria:
- Probabilidad: La probabilidad en las variables discretas se expresacomo Pi=( x=xi)
- Media: Es la esperanza matemática. Fórmula general:

- Varianza: Fórmula general de la varianza y de la desviación típica:
- Distribuciones discretas:
P= probabilidad de que ocurra el suceso A
q= probabilidad de que no ocurra el suceso A; q= 1 - p
Parámetros:
- Distribución binomial:
Parámetros:
Función de probabilidad de la distribución binomial

- Distribuciones continuas:
- Función de densidad: Es una función que cumple que F(x)>0 para cualquier valor de x y que:
La probabilidad P(a < x < b) =
- Distribución normal: Si x es una variable continua, x es normal de media μ y desviación típica σ.


- Tipificación de variables: (μ=0; σ=1)
N(0,1);
- Aproximación de binomial por la normal:
se puede aproximar por la normal cuando se cumpla que nxp>5 y nxq>5, entonces N(np,√npq )
Fuentes: www.wikipedia.org/ www.vitutor.com/ www.lasmatematicas.es/ www.matematicasbachiller.com






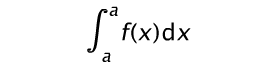




No hay comentarios:
Publicar un comentario