Unidad 9: Funciones elementales.

• Estudio de una función:

El estudio de una función se realiza siguiendo estos pasos:

- Dominio e la función f.

- Asíntotas: Es una recta hacia la que se aproxima una rama infinita de una función. Pueden ser verticales, horizontales y oblicuas.

- Puntos de corte con los ejes: En el eje X son todos los valores de x que cumplen que f(x)=0 y en el eje Y, es el valor y= f(0)

- Signo: Si X1, X2, ... Xn son puntos de corte con el eje X , el signo en (-∞,-x), (X1, X2), ( Xn, +∞) puede cambiar de un intervalo a otro. También se tienen en cuenta las asíntotas verticales, si las hay.

- Simetría: Pueden ser funciones pares (simétricos respecto al eje Y): f(x)= f(-x), funciones impares (simétricos respecto al origen): f(-x)= - f(x) o no tienen simetría.

• Funciones polinómicas:

Son funciones del tipo f(x)= P(x) ; donde P(x) es un polinomio. 

Su dominio son todos los reales; asíntotas no tienen; los puntos de corte con el eje X son las raíces de ese polinomio y con el eje Y es f(0); la simetría depende del polinomio.

También se tiene en cuenta el signo de a (ax2 + bx + c) para ver si la parábola es cóncava o convexa. Se calcula el eje de simetría ( -b/2a) y su vértice ( -b/2a, f(-b/2a)).

Ej: f(x)= x2 - 4

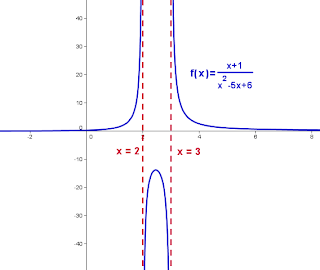
•  Funciones racionales:

Son funciones del tipo f(x)= P(x)/Q(x) ; P(x) y Q(x) son polinomios con el grado de Q(x) mayor o igual a 1.

Su dominio son todos los reales excepto las valores que hacen cero el denominador, es decir, R - { x / Q(x)= 0}. 

Las asíntotas pueden ser verticales (valores que anulan el denominador), horizontales (siempre que P(x) y Q(x) tengan el mismo grado o que el grado de Q(x) sea mayor que el de  P(x)) y oblicuas (si P(x) tiene un grado más que el polinomio Q(x)).

El punto de corte con el eje Y es f(0) y los puntos de corte con el eje X son las raíces del numerador.

La simetría puede ser par, impar o no tener (dependerá de cada función).

El sigo de la función se estudia en los tramos definidos por los puntos de corte con el eje X y los valores que no pertenecen al dominio.

Ej:

• Funciones con radicales:

Una función es radical si la variable independiente aparece dentro de una raíz.

El dominio de la función se calcula imponiendo como condición que lo de dentro de la raíz debe de ser mayor o igual a cero. Los puntos de corte se calculan igualando a cero la función (Eje X) y calculando f(0) (Eje Y). Se calcula si tienen algún tipo de asíntotas y con estas y los puntos de corte se saca el signo. Y se localiza si posee algún tipo de simetría o ninguna. 

Ej:

• Funciones periódicas:

Una función f es periódica si existe un número t, período, que cumple  que f( x + t)= f(x) para todo x perteneciente al dominio.

Ej:

• Funciones exponenciales:

Si a pertenece a los reales a>0 y a es distinto de 0, una función exponencial es del tipo f(x)= ax

Su dominio es igual a R. El punto de corte con el eje Y es siempre el (0, 1) ya que cualquier número elevado a cero es 1.Y con el eje X no existen puntos de corte ya que la ecuación

 ax = 0 no tiene solución. Solo tiene una asíntota horizontal en y= 0. Simetrías no tiene y el signo siempre es positivo. 

Ej:

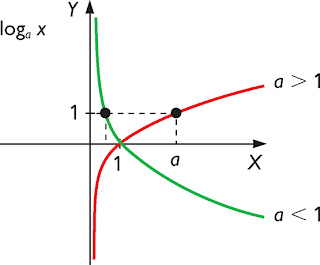
• Funciones logarítmicas:

Si a pertenece a los números reales con a>0 y a distinto que 1, una función logarítmica es del tipo f(x)= loga x

Su dominio es siempre (0, + ∞).corta con el eje X en el (1, 0) y con el eje Y no corta. Tiene solo una asíntota vertical en x= 0

La función exponencial y la logarítmica, cuando tienen sus bases iguales, son inversas y se comprueba haciendo la composición de funciones y también gráficamente.

Ej:

 

Esta función representa a f(x)= e^x y a su inversa, f(x)= ln x, con el eje de simetría y= x.

• Funciones trigonométricas:

- Función seno: f(x)= sen x

Su dominio son todos los reales, la Im(f)= [-1, 1]. Los puntos de corte con el eje X son todos aquellos valores que cumplen que sen x= 0 y el punto de corte con el eje Y es el (0, 0). Es una función periódica con t=.La simetría es impar.

- Función coseno: f(x)= cos x

Dom(f)= R y recorrido es [-1, 1]. Corta al eje Y en el puto (0, 1) y al eje X cuando la función se iguala a cero. Tiene el mismo período que la función f(x)= sen x. Está adelantada 90º( en radianes) de la función sen x. La simetría es par.

- Función tangente: f(x)= tg x

Dom(f)= R - {los valores que hacen cero el denominador ya que tan x= sen x/cos x} y Im(f)=[-1, 1]. Tiene asíntotas verticales en cada uno de los valores que anulan el denominador. Es una función con período t=.

Los puntos de corte con el eje X son todos aquellos que se calculan cuando tg x= 0 y el punto de corte con el eje Y es el (0, 0). Su simetría es impar.

• Traslación y dilatación de funciones: