Unidad 7: Números complejos.

El primero en usar los números complejos fue el matemático italiano G. Cardano (Siglo XVI) quien encontró la formula para resolver las ecuaciones cúbicas. El termino “numero complejo” fue introducido por el gran matemático alemán C.F. Gauss (siglo XVIII-XIX) cuyo trabajo fue de importancia básica en álgebra, teoría de los números, ecuaciones diferenciales, geometría diferencial, geometría no eclidiana, análisis complejo, análisis numérico y mecánica teórica, también abrió el camino para el uso general y sistemático de los números complejos.                

 Un número complejo es aquel que describe la suma de un número real y un número imaginario, como por ejemplo a + bi ; donde a y b son números reales e i= √-1. Ej: 1 + 3i ; 5 - 2i; 5i ( imaginario puro). Las raíces de números negativos no tenía solución el los R, pero en los C si la tienen, como √-3= √3i. 

                                         z = a + bi ; Forma binómica

Al componente a se le denomina como parte real (Re(z))y el componente b es la parte imaginaria (Im(z)). Dos números complejos son iguales si sus partes real e imaginaria coinciden, es decir, z=a + bi es igual a z'=a' + b'i si a=a' y b=b'.

Ej: z = 2 + 5i y z' = 2 + 5i son iguales.

• Conjugado y opuesto de un número complejo:

El conjugado de un número complejo es el mismo, pero su parte imaginaria con signo contrario. Se expresa como z.

Ej: z = 3 + 4i    ;    z= 3 - 4i

El opuesto es aquel número complejo cambiado de signo, es decir, si z= a + bi ; -z= -a - bi.

Ej: op(3 - 2i)= -3 + 2

• Módulo de un complejo:

El módulo de un complejo se define como:  

Ej: 3 + 4i ;  |z| = 5.

• Representación gráfica: Plano complejo.

Si tomamos como ejemplo z = 2 + 3i, si afijo sería (2,3); las coordenadas. Su módulo sería la distancia desde el afijo hasta el (0,0).

• Operaciones con números complejos:

- Suma: Si z= a + bi y z'= a' + b'i se define como z + z'= (a + a') + (b + b')i

Ej: (2 + i) + (5 - 3i) = 7 - 2i

- Resta: Si z= a + bi y z'= a' + b'i se define como z - z'= (a - a') + (b - b')i

                                                                                            

- Producto:Si z= a + bi y z'= a' + b'i definimos la multiplicación como

               z x z= (a + bi)(a' + b'i) = (aa' - bb') + (ba' + ab')i

Ej: (7 - 4i)(2 + 3i) = (14 + 12) + (21 - 8)i = 26 + 13i

- Cociente:Si  z= a + bi, el inverso es z^- = 1/z
z^-1 = (a - bi) / (a² + b²)

 - Potencias de i:

i⁰= 1         i⁴= 1         

i¹= i          i⁵= i

i²= -1        i⁶= -1

i³= -i         ...

Ej: i^{342,se realiza haciendo la división del exponente entre cuatro (siempre). Cuando obtenemos el resto, elevamos a i a dicho número y luego consultamos el resultado en la tabla anterior.Por lo tanto,} i^{342 =} i²= -1.

• Forma polar de un número complejo:

Si z= a + bi es un número complejo con |z|=r y argumento α=tg a/b, entonces z se puede poner como z=r_α.

- Paso de  forma polar a forma binómica:

Ej:  2_30º

Re(z): cos 30º= Re(z)/2    ;  Re(z)= 2 x cos 30º

Im(z): sen 30º= Im(z)/2    ;  Im(z)= 2 x sen 30º

z= 2 x cos 30º + (2 x sen 30º)i : Forma trigonométrica

z= 2(cos30º + sen30ºi)

z= 2(√3/2 + 1/2i)      z= √3 + i

• Operaciones en forma polar:

Las operaciones que se realizan en forma polar son:

- Producto:

Ej: z= 2_30º       z x z'= (2x3)15+30 =6_45º

     z'= 3_15º

- Cociente:

Ej: z= 2_30º       z / z'= (2/3)15-30 =(2/3)_15º

     z'= 3_15º

- Potencia:

Ej:z4= 2⁴30ºx4 =16_120º

• Raíces de complejos en forma polar:

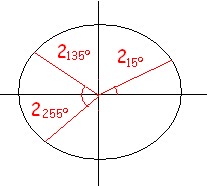
Ej:3√8_45º : 2_15º ;  2_120º ;  2_255º

                                       

• Raíces de un polinomio:

 - Teorema fundamental del álgebra: Todo polinomio de grado n tiene n raíces en C.

Ej: 2x³ + 14x² + 32x + 20 = 0

Sacamos por Ruffini la primera raíz x=-1y así obtenemos un polinomio de 2º grado que se resuelve mediante la fórmula general. De esta manera, se obtienen las dos raíces restantes, que son: x= -3 - 2i ; x= -3 + 2i (son conjugados si tienen coeficientes reales; propiedad de la conjugación).